Bisector fields and projective duality, arXiv:2306.08612
Authors: Bruce Olberding, Elaine A. Walker
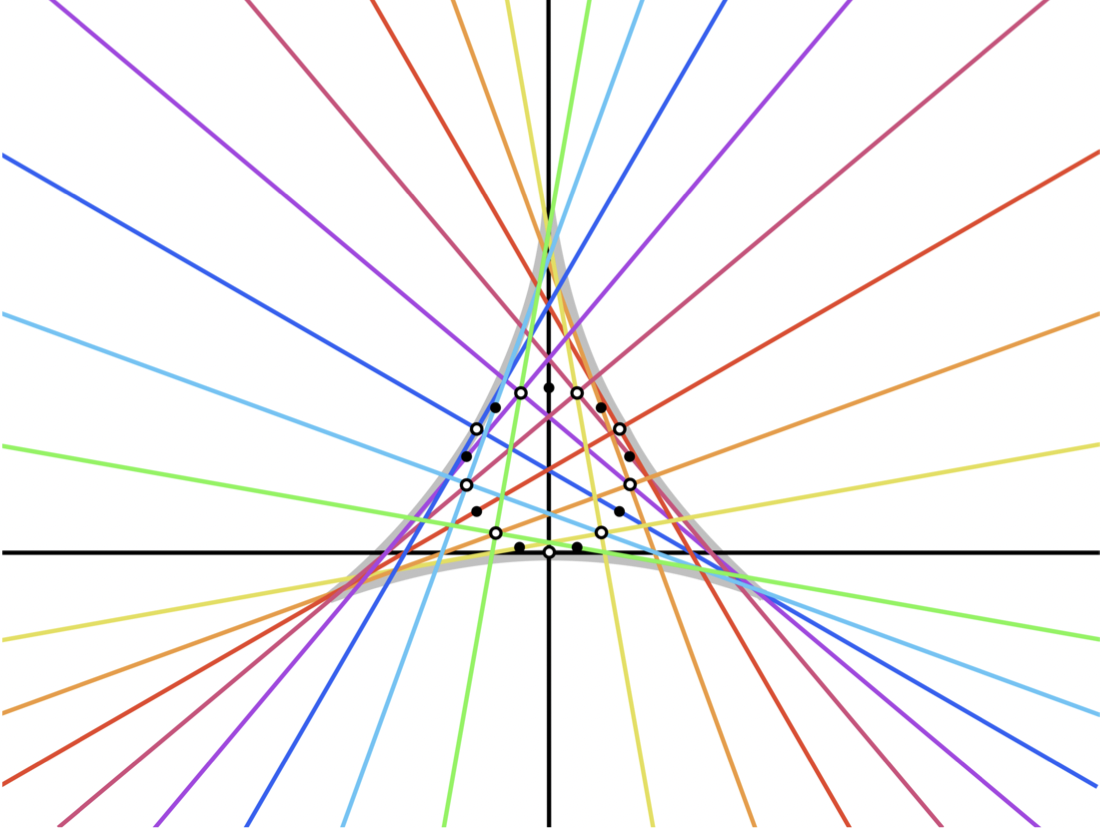
Abstract. Working over a field k of characteristic ≠ 2, we study what we call bisector fields, which are arrangements of paired lines in the plane that have the property that each line in the arrangement crosses the paired lines in pairs of points that all share the same midpoint. To do so, we use tools from the theory of algebraic curves and projective duality. We obtain a complete classification if k is real closed or algebraically closed, and we obtain a partial classification if k is a finite field. A classification for other fields remains an open question. Ultimately this is a question regarding affine equivalence within a system of certain rational quartic curves.
Submitted 14 June, 2023; originally announced June 2023.
Authors: Bruce Olberding, Elaine A. Walker
Abstract. Working over a field k of characteristic ≠ 2, we study what we call bisector fields, which are arrangements of paired lines in the plane that have the property that each line in the arrangement crosses the paired lines in pairs of points that all share the same midpoint. To do so, we use tools from the theory of algebraic curves and projective duality. We obtain a complete classification if k is real closed or algebraically closed, and we obtain a partial classification if k is a finite field. A classification for other fields remains an open question. Ultimately this is a question regarding affine equivalence within a system of certain rational quartic curves.
Submitted 14 June, 2023; originally announced June 2023.
Bisector fields of quadrilaterals, Contributions to Algebra and Geometry (2024)
Authors: Bruce Olberding, Elaine A. Walker
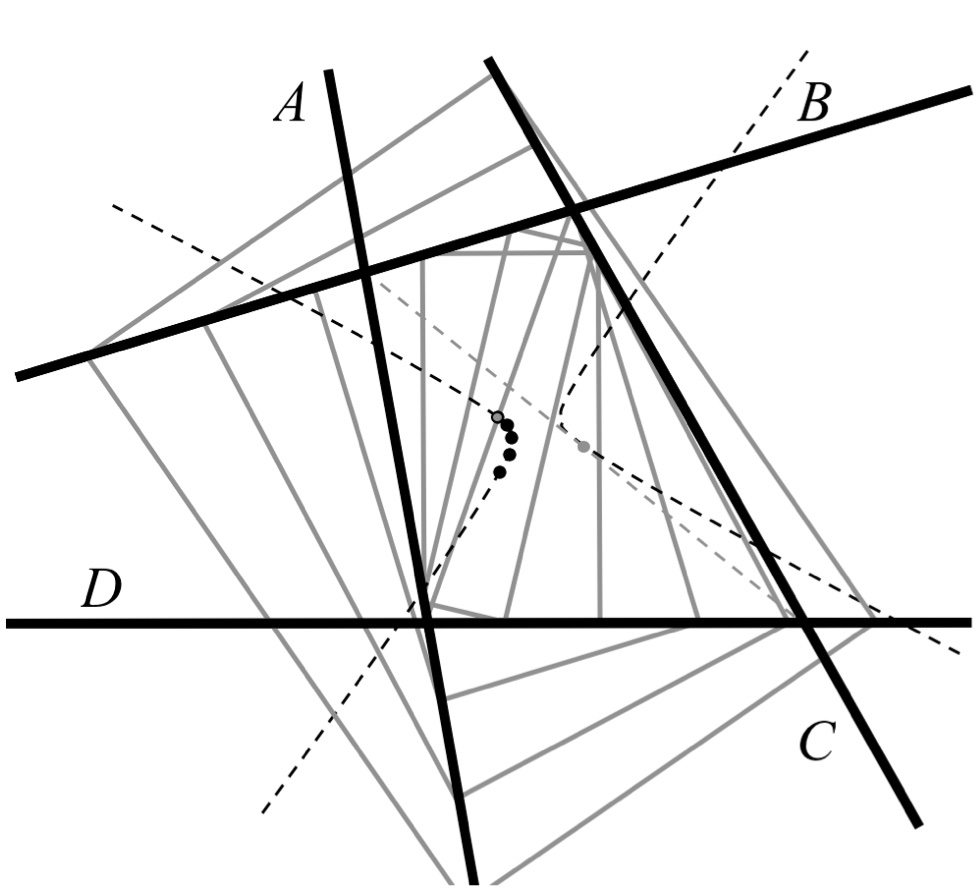
Abstract: A bisector field is a maximal set B of paired lines in the plane such that each line in each pair crosses the other pairs in B in pairs of points that all share the same midpoint. We showed in a previous article that bisector fields are precisely the sets of pairs of lines that occur as asymptotes of hyperbolas from a pencil of affine conics, along with pairs of parallel lines arising from degenerate parabolas in the pencil. In this article we give a different application, this time to complete quadrilaterals and their nine-point conics. We show that every complete quadrilateral generates a bisector field as the set of bisectors of the quadrilateral paired according to an orthogonality condition in a geometry determined by the quadrilateral. The nine-point conic, so named because it passes through nine distinguished points of the quadrilateral, is shown to be the locus of midpoints of the bisector field associated to the quadrilateral, thus giving an interpretation of the other points on the nine-point conic. Our approach is analytic, and our results hold over any field of characteristic other than 2.
Submitted 19 May, 2023; originally announced May 2023.
Authors: Bruce Olberding, Elaine A. Walker
Abstract: A bisector field is a maximal set B of paired lines in the plane such that each line in each pair crosses the other pairs in B in pairs of points that all share the same midpoint. We showed in a previous article that bisector fields are precisely the sets of pairs of lines that occur as asymptotes of hyperbolas from a pencil of affine conics, along with pairs of parallel lines arising from degenerate parabolas in the pencil. In this article we give a different application, this time to complete quadrilaterals and their nine-point conics. We show that every complete quadrilateral generates a bisector field as the set of bisectors of the quadrilateral paired according to an orthogonality condition in a geometry determined by the quadrilateral. The nine-point conic, so named because it passes through nine distinguished points of the quadrilateral, is shown to be the locus of midpoints of the bisector field associated to the quadrilateral, thus giving an interpretation of the other points on the nine-point conic. Our approach is analytic, and our results hold over any field of characteristic other than 2.
Submitted 19 May, 2023; originally announced May 2023.
Bisector fields and pencils of conics, arXiv:2305.08324
Authors: Bruce Olberding, Elaine A. Walker
Abstract: Working over a field of characteristic other than 2, we show that the degenerations of the conics in a nontrivial pencil of affine conics form an arrangement of pairs of lines that we call a bisector field, a maximal set B of paired lines such that each line in B simultaneously bisects each pair in B. Conversely, every bisector field arises this way from a pencil of affine conics.
Submitted 14 May, 2023; originally announced May 2023.
Authors: Bruce Olberding, Elaine A. Walker
Abstract: Working over a field of characteristic other than 2, we show that the degenerations of the conics in a nontrivial pencil of affine conics form an arrangement of pairs of lines that we call a bisector field, a maximal set B of paired lines such that each line in B simultaneously bisects each pair in B. Conversely, every bisector field arises this way from a pencil of affine conics.
Submitted 14 May, 2023; originally announced May 2023.
Rectangles conformally inscribed in lines
J. Geom. 113, 9 (2022)
Authors: Bruce Olberding, Elaine A. Walker
Abstract: A parallelogram is conformally inscribed in four lines in the plane if it is inscribed in a scaled copy of the configuration of four lines. We describe the geometry of the three-dimensional Euclidean space whose points are the parallelograms conformally inscribed in sequence in these four lines. In doing so, we describe the flow of inscribed rectangles by introducing a compact model of the rectangle inscription problem.
Submitted 2 August, 2021; originally announced August 2021.
J. Geom. 113, 9 (2022)
Authors: Bruce Olberding, Elaine A. Walker
Abstract: A parallelogram is conformally inscribed in four lines in the plane if it is inscribed in a scaled copy of the configuration of four lines. We describe the geometry of the three-dimensional Euclidean space whose points are the parallelograms conformally inscribed in sequence in these four lines. In doing so, we describe the flow of inscribed rectangles by introducing a compact model of the rectangle inscription problem.
Submitted 2 August, 2021; originally announced August 2021.
Paths of rectangles inscribed in lines over fields
Beitr Algebra Geom (2022)
Authors: Bruce Olberding, Elaine A. Walker
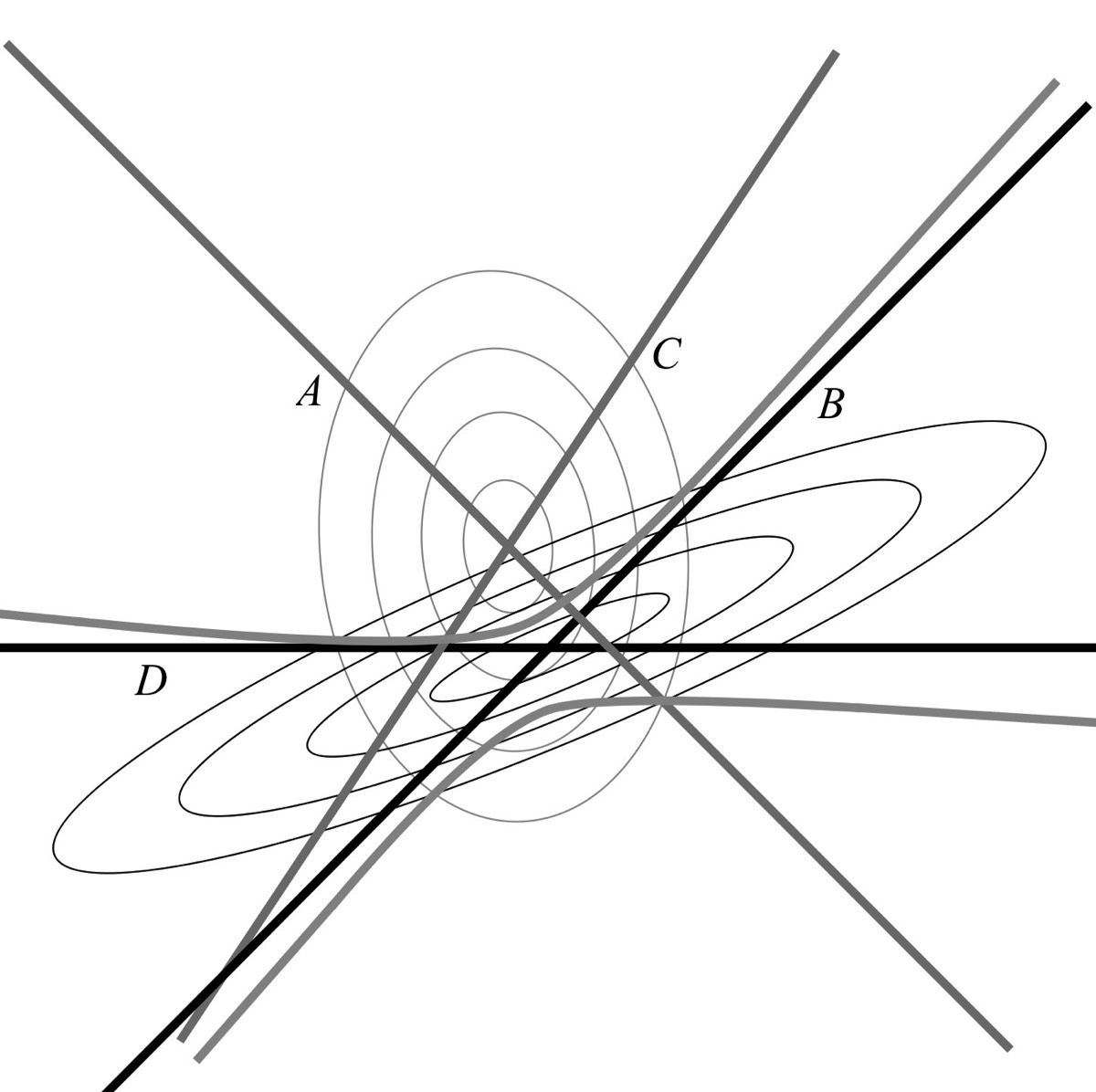
Abstract: We study rectangles inscribed in lines in the plane by parametrizing these rectangles in two ways, one involving slope and the other aspect ratio. This produces two paths, one that finds rectangles with specified slope and the other rectangles with specified aspect ratio. We describe the geometry of these paths and its dependence on the choice of four lines. Our methods are algebraic and work over an arbitrary field.
Submitted 16 December, 2020; v1 submitted 25 June, 2020; originally announced June 2020.
Beitr Algebra Geom (2022)
Authors: Bruce Olberding, Elaine A. Walker
Abstract: We study rectangles inscribed in lines in the plane by parametrizing these rectangles in two ways, one involving slope and the other aspect ratio. This produces two paths, one that finds rectangles with specified slope and the other rectangles with specified aspect ratio. We describe the geometry of these paths and its dependence on the choice of four lines. Our methods are algebraic and work over an arbitrary field.
Submitted 16 December, 2020; v1 submitted 25 June, 2020; originally announced June 2020.
The conic geometry of rectangles inscribed in lines
Proc. Amer. Math. Soc. 149 (2021), 2625-2638
Authors: Bruce Olberding, Elaine A. Walker
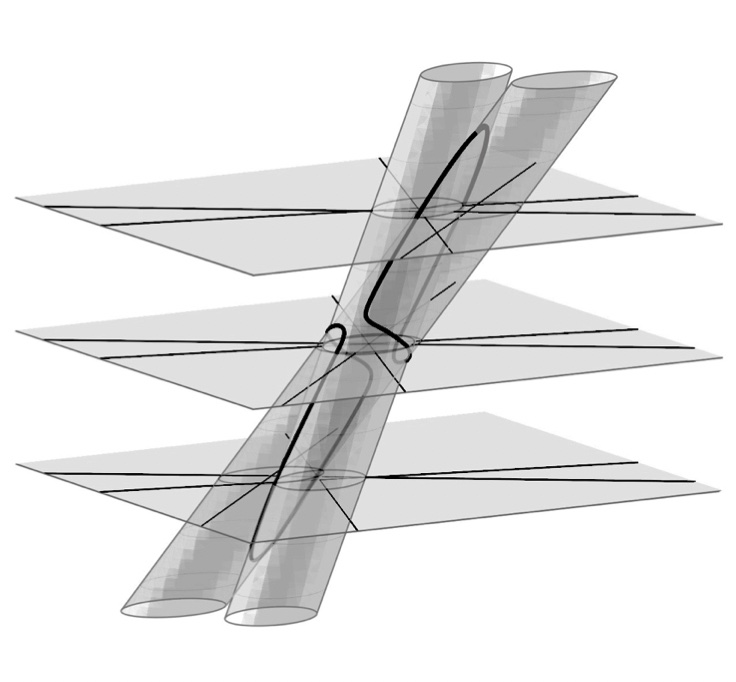
Abstract: We develop a circle of ideas involving pairs of lines in the plane, intersections of hyperbolically rotated elliptical cones and the locus of the centers of rectangles inscribed in lines in the plane.
Submitted 2 August, 2021; v1 submitted 15 August, 2019; originally announced August of 2019.
Proc. Amer. Math. Soc. 149 (2021), 2625-2638
Authors: Bruce Olberding, Elaine A. Walker
Abstract: We develop a circle of ideas involving pairs of lines in the plane, intersections of hyperbolically rotated elliptical cones and the locus of the centers of rectangles inscribed in lines in the plane.
Submitted 2 August, 2021; v1 submitted 15 August, 2019; originally announced August of 2019.